[home: :posts: :subscribe]

encrypting secrets in memory

July 18th, 2019

In a previous post I talked about designing and implementing an in-memory data structure for storing sensitive information in Go. The latest version of memguard adds something new: encryption.

But why? Well, there are limitations to the old solution of using guarded heap allocations for everything.

  1. A minimum of three memory pages have to be allocated for each value: two guard pages sandwiching n≥1 n \geq 1 data pages.
  2. Some systems impose an upper limit on the amount of memory that an individual process is able to prevent from being swapped out to disk.
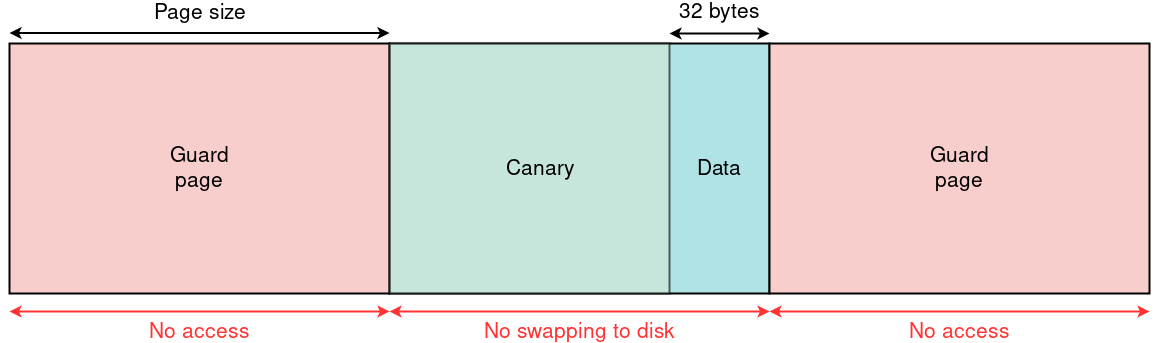
Memory layout of guarded heap allocation.

Typical layout of a 32 byte guarded heap allocation.

So it is worth looking into the use of encryption to protect information. After all, ciphertext does not have to be treated with much care and authentication guarantees immutability for free. The problem of recovering a secret is shifted to recovering the key that protects it.

But there is the obvious problem. Where and how do you store the encryption key?

We use a scheme described by Bruce Schneier in Cryptography Engineering. The procedure is sometimes referred to as a Boojum. I will formally define it below for convenience.

Define B={i:0≤i≤255} B = \{i : 0 \leq i \leq 255\} to be the set of values that a byte may take. Define h:Bn→B32 h : B^n \to B^{32} for n∈N0 n \in \mathbb{N}_0 to be a cryptographically-secure hash function. Define the binary XOR operator ⊕:Bn×Bn→Bn \oplus : B^n \times B^n \to B^n .

Suppose k∈B32 k \in B^{32} is the key we want to protect and Rn∈B32 R_n \in B^{32} is some random bytes sourced from a suitable CSPRNG. We initialise the two partitions:

x1=R1y1=h(x1)⊕k \begin{aligned} x_1 &= R_1\\ y_1 &= h(x_1) \oplus k\\ \end{aligned}

storing each inside its own guarded heap allocation. Then every m m milliseconds we overwrite each value with:

xn+1=xn⊕Rn+1=R1⊕R2⊕⋯⊕Rn+1yn+1=yn⊕h(xn)⊕h(xn+1)=h(xn)⊕h(xn)⊕h(xn+1)⊕k=h(xn+1)⊕k \begin{aligned} x_{n+1} &= x_n \oplus R_{n+1}\\ &= R_1 \oplus R_2 \oplus \cdots \oplus R_{n+1}\\ y_{n+1} &= y_n \oplus h(x_n) \oplus h(x_{n+1})\\ &= h(x_n) \oplus h(x_n) \oplus h(x_{n+1}) \oplus k\\ &= h(x_{n+1}) \oplus k\\ \end{aligned}

and so on. Then by the properties of XOR,

k=h(xn)⊕yn=h(xn)⊕h(xn)⊕k=0⊕k=k \begin{aligned} k &= h(x_n) \oplus y_n\\ &= h(x_n) \oplus h(x_n) \oplus k\\ &= 0 \oplus k\\ &= k\\ \end{aligned}

It is clear from this that our iterative overwriting steps do not affect the value of k k , and the proof also gives us a way of retrieving k k . My own implementation of the protocol in fairly idiomatic Go code is available here.

An issue with the Boojum scheme is that it has a relatively high overhead from two guarded allocations using six memory pages in total, and we have to compute and write 64 bytes every m m milliseconds. However we only store a single global key, and the overhead can be tweaked by scaling m m as needed. Its value at the time of writing is 8 milliseconds.

The authors of the Boojum claim that it defends against cold boot attacks, and I would speculate that there is also some defence against side-channel attacks due to the fact that k k is split across two different locations in memory and each partition is constantly changing. Those attacks usually have an error rate and are relatively slow.

OpenBSD added a somewhat related mitigation to their SSH implementation that stores a 16 KiB (static) “pre-key” that is hashed to derive the final key when it is needed. I investigated incorporating it somehow but decided against it. Both schemes have a weak point when the key is in “unlocked” form so mimimising this window of opportunity is ideal.

In memguard the key is initialised when the program starts and then hangs around in the background—constantly flickering—until it is needed. When some data needs to be encrypted or decrypted, the key is unlocked and used for the operation and then it is destroyed.

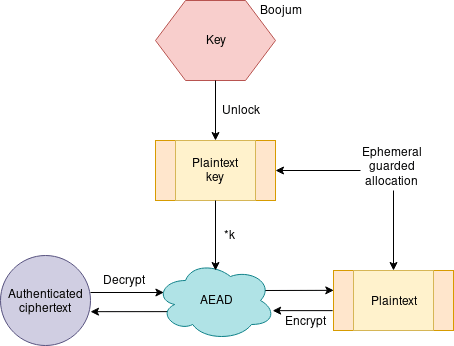
Diagram showing the high-level structure of the scheme.

High-level overview of the encryption scheme.

The documentation provides a relatively intuitive guide to the package’s functionality. The Enclave stores ciphertext, the LockedBuffer stores plaintext, and core.Coffer implements the Boojum. Examples are available in the examples sub-package.

The most pressing issue at the moment is that the package relies on cryptographic primitives implemented by the Go standard library which does not secure its own memory and may leak values that are passed to it. There has been some discussion about this but for now it seems as though rewriting crucial security APIs to use specially allocated memory is the only feasible solution.

If you have any ideas and wish to contribute, please do get in touch or open a pull request.

{home : : subscribe with rss/atom}